皆さんは微分がどんな場面で使われているか知っていますか?
微分なんて使わないぜ!と思っている人の周りにも微分はこっそり使われてる。
例えば……….
車のスピードメーターとか
経済やビジネスの分析とか
ゲームの物理エンジンとか



元々はかの有名なアイザック・ニュートンが惑星の軌道を計算したくて使ってたのが微分。
微分ができると物体の運動が予測できるので、軍が砲弾撃つ時にも微分は欠かせない。
今回はそんな売れっ子タレント”微分さん”を3ステップでわかりやすく解説します。
1, 一言でいうと微分とは……
2, 微分公式を簡単に求めてみる
3, 実際に微分を使ってみる!
1, 一言でいうと微分とは……
”傾き(速度)を求めるツール”である
例えば、科学者たちが新型乗り物の実験でデータを取っていて
乗り物の進んだ距離がこんな風に変化したとする。
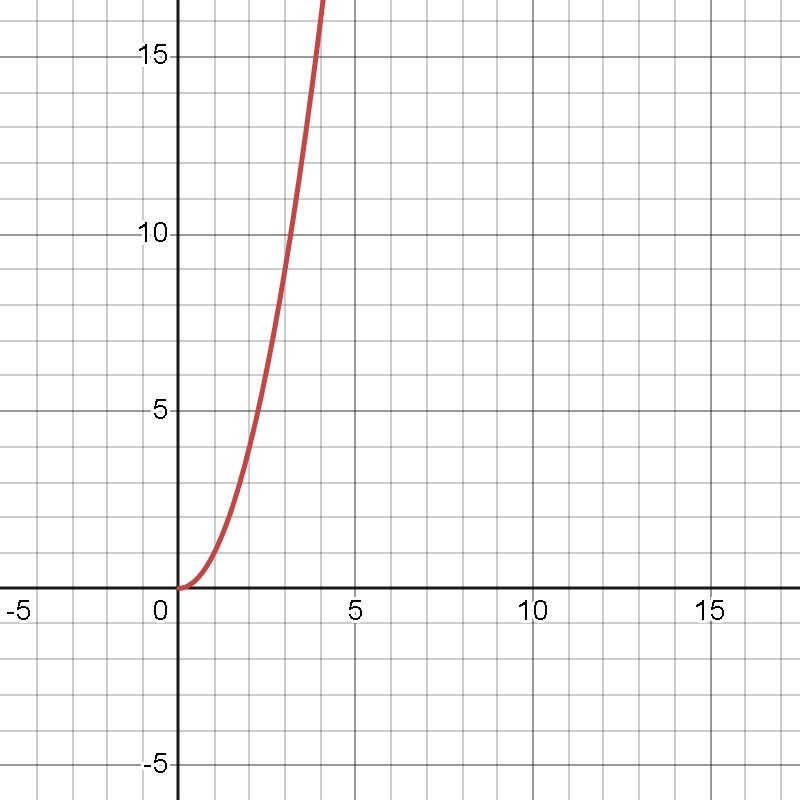
Y=X2のグラフ(X≧0)
縦:乗り物の進んだ距離(m)
横:時間(秒)
1秒後には1m(スタート地点からの距離)、2秒後には4m、3秒後には9mのところまで進んでいてどんどん速くなっていく乗り物。
じゃあ、3秒後(9mまで進んだ時点)の乗り物の速度はどのくらいだろう?
速度を求めるには、距離を時間で割ればいいから9÷3で秒速3mだぁー!!!(ドヤッ)
とはならないんですね。
なぜならコイツは直線ではなく曲線で、毎秒速度が変わってるから単純な距離÷時間じゃわからない。
でも、僕たちが使えるのはこのグラフと四則演算(+ー✖÷)だけ!
一体どうしたらいいんだーーーーー(絶望)
という時に使えるのが微分なのです!
2, 微分公式を簡単に求めてみる
では、どうしたら乗り物の速度を求められるのか?

Y=X2のグラフ(X≧0)
縦:乗り物の進んだ距離
横:時間(秒)
もし、このグラフが直線なら 縦(距離)÷ 横(時間)= 傾き(速度)なので傾きを求めれば速度が求まる。
つまり、当たり前だけど直線なら速度が求まるんです。(大事なことなので2度言いました)
そこで、3秒の時のグラフをめちゃくちゃズームしてみると……
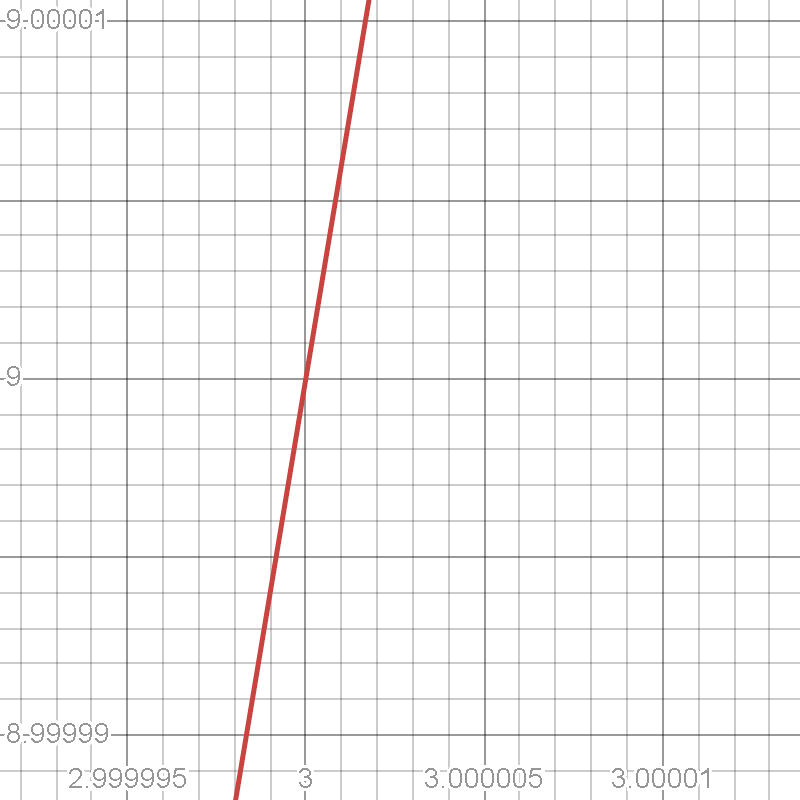
↑3秒のところを超ズームしたグラフ
(1マスの長さが0.0000001みたいに小さくなるほど)
なんか直線ぽいのが見えますよね、これの傾きを求めれば速度が求まりそうです。
じゃあ、具体的にどうやって求めるかというと
まず縦÷横をするために横の長さをα、縦の長さを(3+α)2ー(3)2とします。
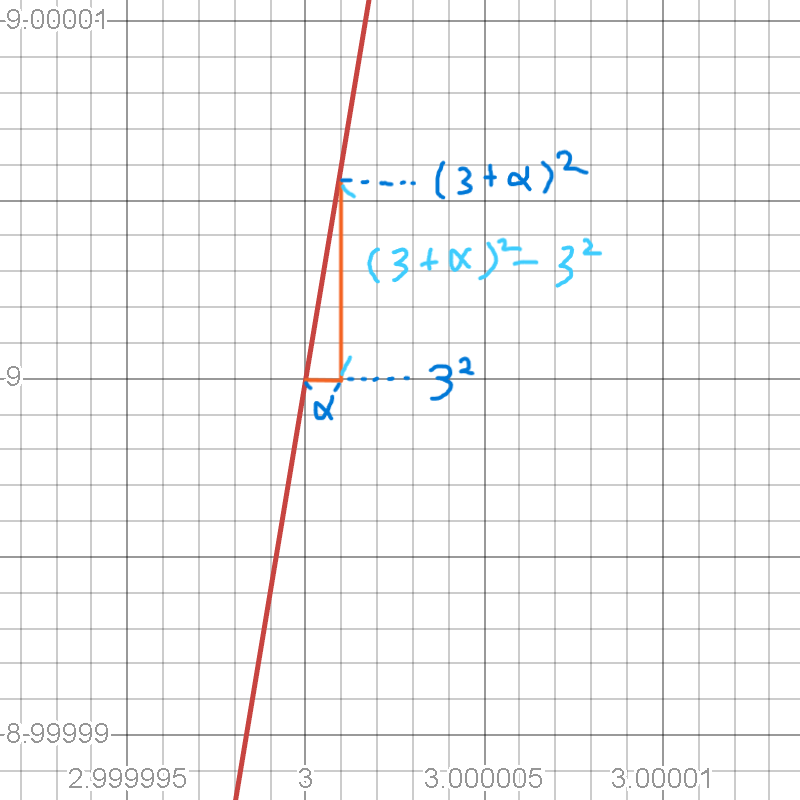
そしたら、傾き(速度)=縦÷横なので、速度は、
この式を展開して計算すると、
となります。
最後に、この α は超ズームしてるグラフの物なので α は実質0ということになるので
つまり、3秒の時の傾き(速度)は6ということが分かって大団円というわけです!
ここまでのポイントをまとめると、
1,傾きを求めれば速度が求まる
2,曲線だと求められないからめっちゃズームして直線を見つける
3,横の長さを極限まで0に近い α として縦÷横をして傾きを求める
今やったこの作業こそが微分というものなんですね。
この式を3(秒)以外にも当てはめるために文字を使って表すと、
Xの部分に数(今回なら3)を当てはめてlim(極限)って記号で α を0に近づけます。
数式にすると難しく感じるかもしれないけど、やってることはさっきと同じ!
因みに、実際にこの数式を計算すると、
となります。
X に3を当てはめてみると
になるので結局やってることは一緒です!
これであなたも微分マスター!
3, 実際に微分を使ってみる!
ここからは実際の例で微分を使っていきます。
と、その前に微分には実はすごく簡単な計算方法があるのです!
例えば、
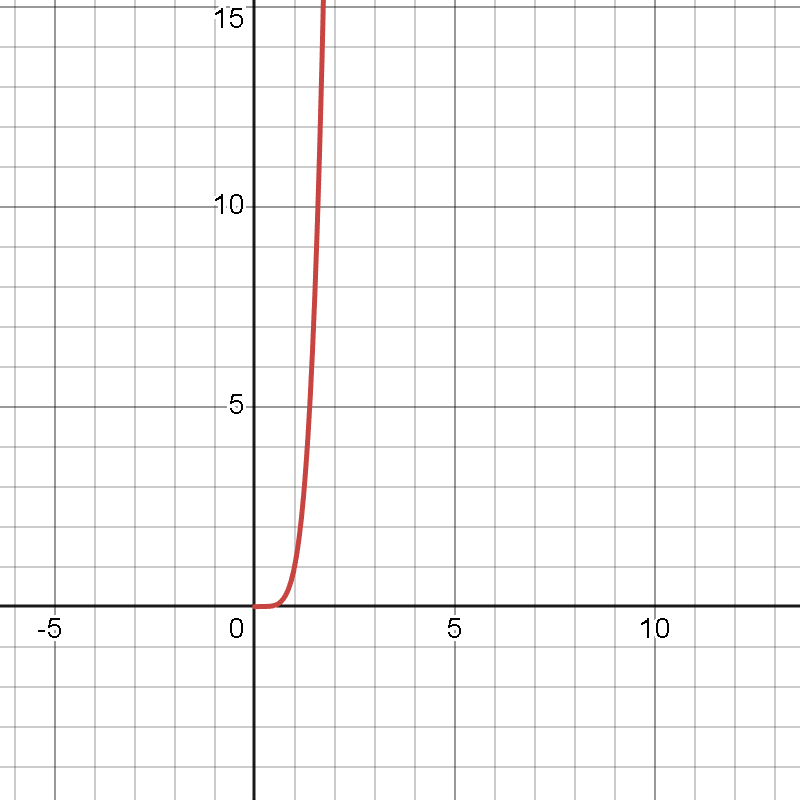
Y=X5のグラフ(X≧0)
こいつをさっきのやり方で微分しようとすると、
となります。
……なんか大変そうですよね。
しかし、これを簡単にする魔法のテクニックがあります。
の5をxの左に持ってきて、5から1減らして4にするんです。
終わり!
これでもう微分完了で、5x4が答えです
さっきのx2も2をxの左に持ってきて1減らしたら
となってさっきと同じ答えが簡単に導けました。
今後は、このやり方を使って問題を解いていきます。
実例
あるカフェで1日100杯の500円のコーヒーが売れる。
20円値上げするたびに売れるコーヒーが2杯少なくなる場合、全体の売り上げが最大になるのはコーヒーが何円の時か?
20円値上げする回数をxとして式にすると
こいつを微分すると、定数(今回なら50000)は0になるので
となります。
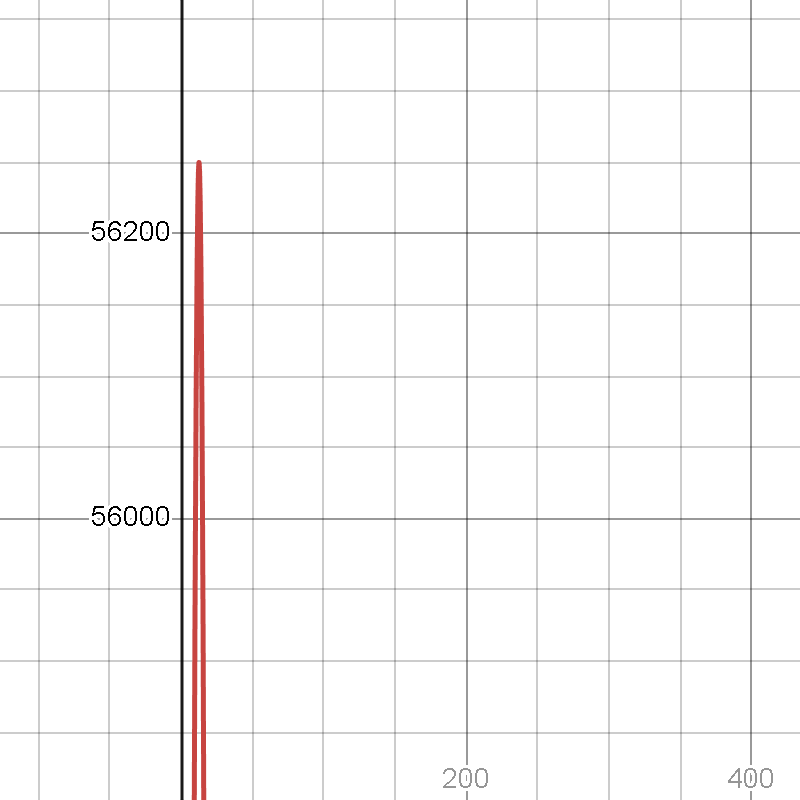
頂点で折れ曲がってる(傾きが+からーになってる)
ここでグラフを見ると、この傾きが+からーになる瞬間が売り上げ最大の時なので
つまり、12.5回20円の値上げをしたところで売り上げが最大になるとわかります。
なので、
つまり750円がコーヒーの値段の最適解ということになるのです!
因みに750円の時の売り上げは75杯売れて56250円です。
こんな感じで傾きが分かると嬉しい時って結構あるんですね。
グラフにできるものには大体微分が使えます。
株価のグラフとかダイエットの時の体重グラフなんかでも微分を使うと傾き、つまるところ今の調子が見えてくるわけですね。
正直、公式とかは気が向いたら覚えればいいので、とりあえず微分ってこういうものなんだなーと思っておくと、日常生活の中に微分が使えるシーンを見つけたり見つけなかったりするので、仕組みだけでも覚えて帰ってくれると嬉しいです!